Abbott Analytical Products



Technical Discussion

Contents of Page

This web page contains a set of technical discussion sections that attempt to establish Charge/Discharge characteristics of the Floating Gate Electron Reservoir Power Source. This discussin starts with the individual cell unit and propagates to the macro-assembly level.

Cullinan Thesis:

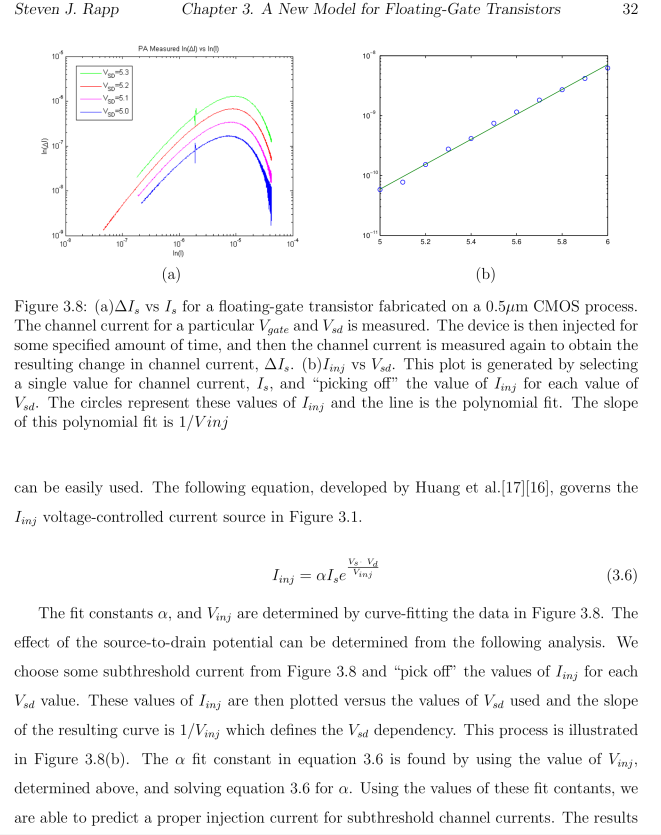
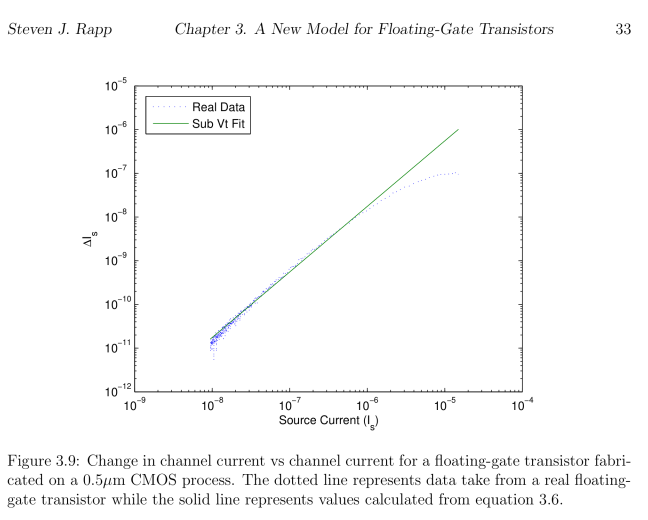
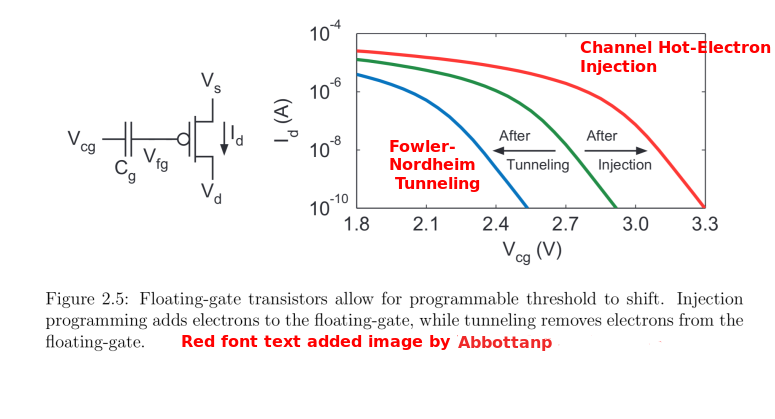
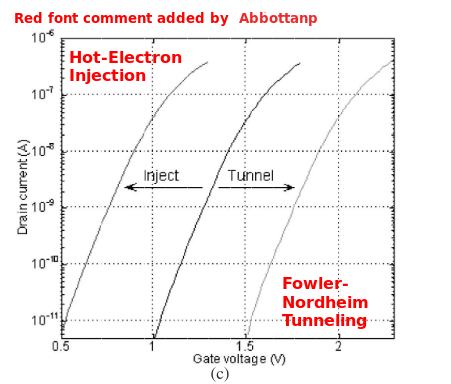
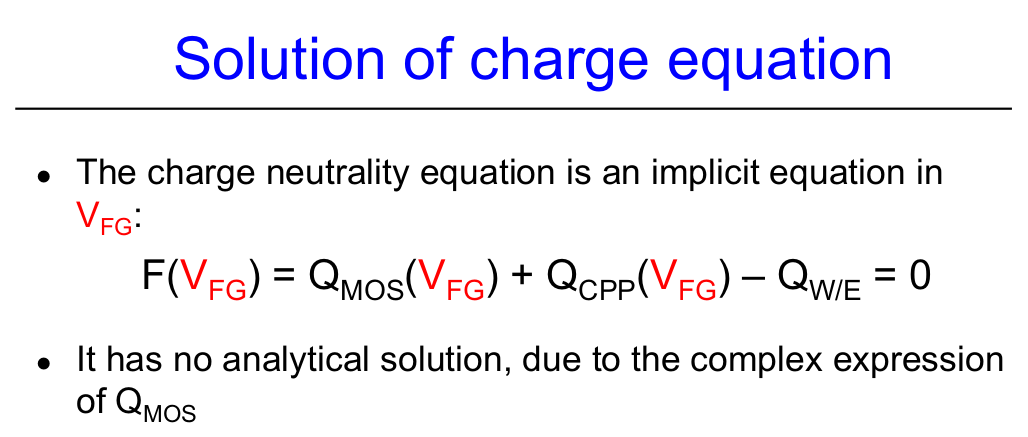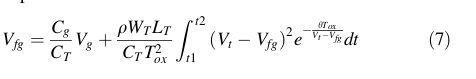Image Comment
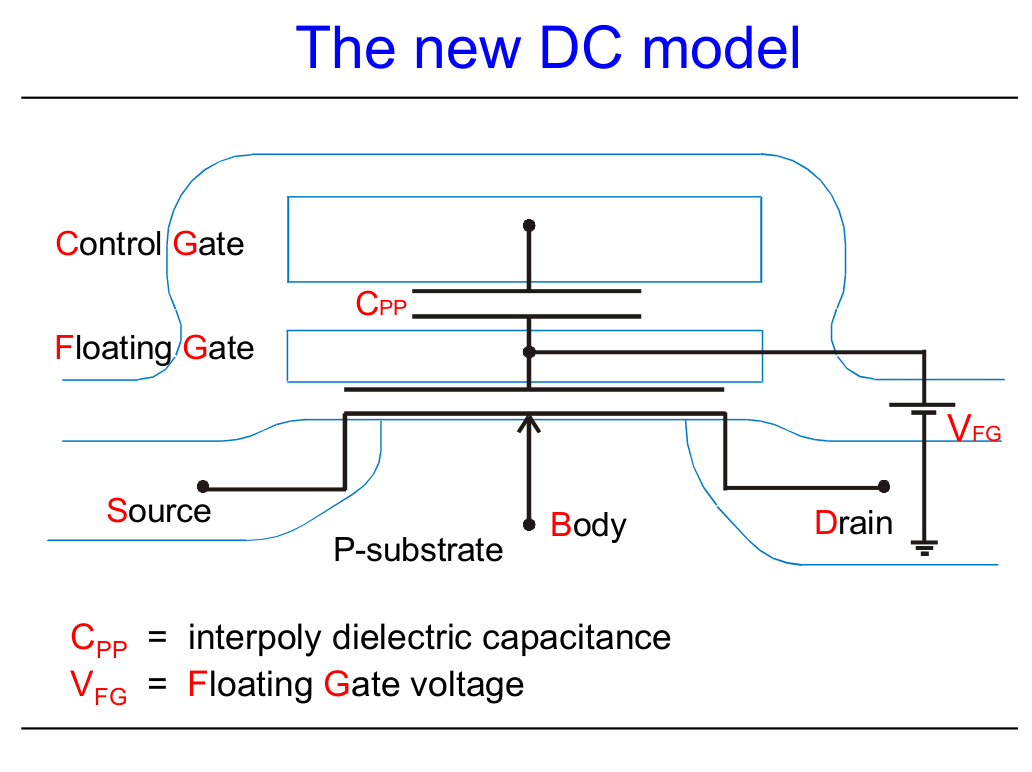
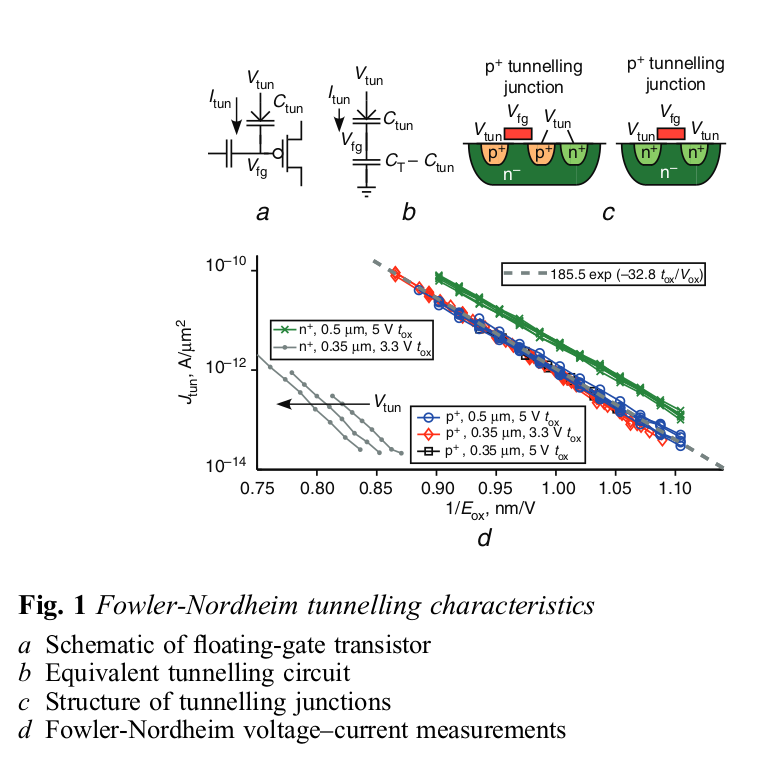
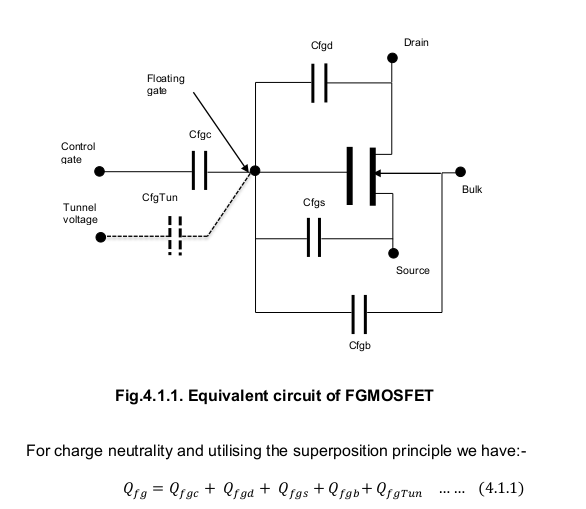
Part 1 page 34 Fig 4.1.1 Eqn 4.1.1. Note the capicator indexing and the charge neutrality equation Eqn 4.1.1.
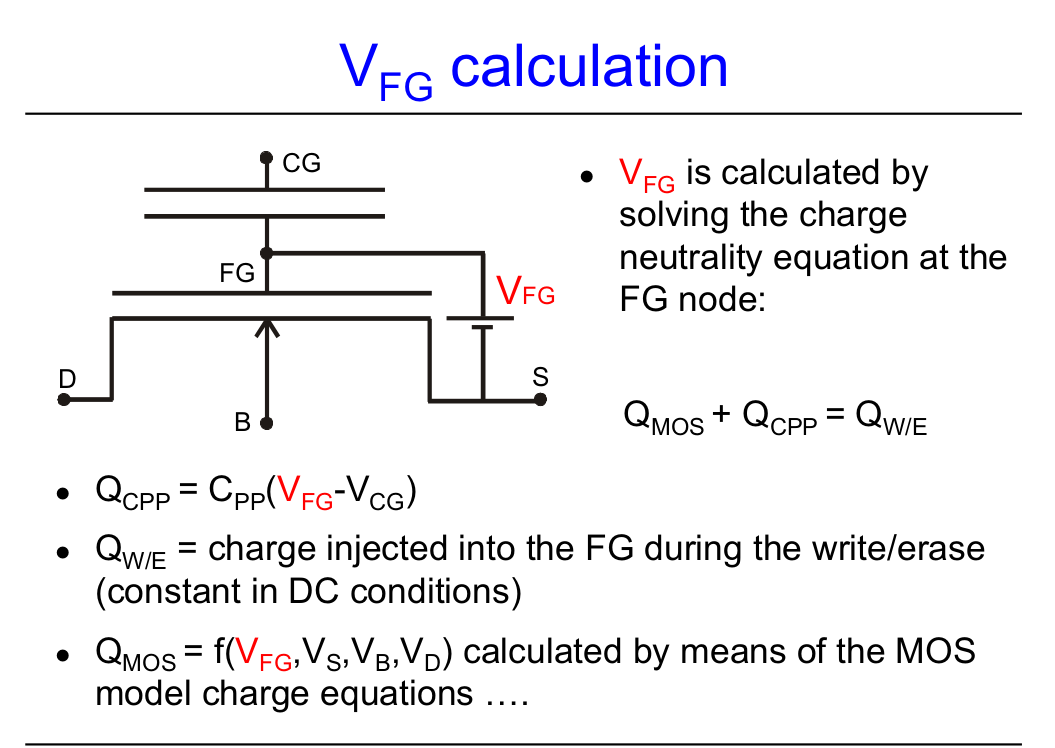
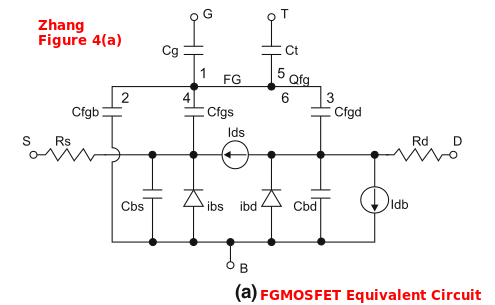
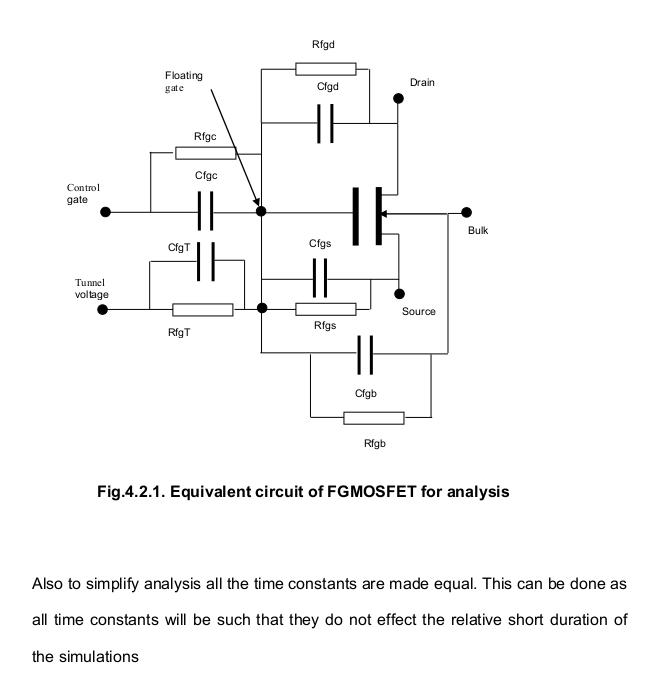
Part 1 page 36 Fig 4.2.1. Using the C=Q/V relationship Fig 4.2.1 is presented as the Equivalent circuit of a FGMOSFET. A shewd constraint is set on all time constants as being equal and large. This removes a level of complexity from the analysis if the "simulations runs" are required to be of relatively short in duration. Note the isolation of the Floating Gate node near the center of the image
Part 1 page 38 Eqn 4.2.9. For the DC or Steady State operationa mode, following a stepwise set of redefinfitons and assumptions Eqn 4.2.9 was derviced. This equation depicts the direct relationship between the Control Gate voltage and the Floating Gate. This condition exist even though no direct measurement of the floating gate is possible.
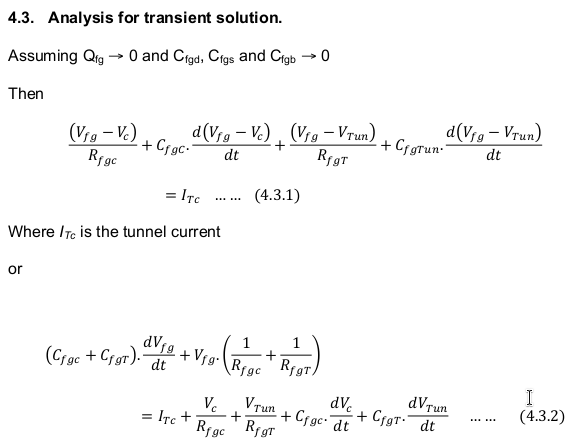
Part 1 page 38 Eqn 4.3.2. The complex nature of Floating Gate Voltage, Eqn 4.3.2, precludes an analytical solution at this time. However, it is demonstrated within the thesis that a suitable Equation Derived Design can be developed to provide a 'close' approximation of a FGMOSFET Transient Solution. For charging the model incorporates the Fowler-Nordheim localized current density, i.e. electron tunneling for charging or charge. This event is often termed programming.

The corresponding compliment, discharing or discharge, is mentioned in the thesis as Channel Hot Electrons. The third term usually associated with charge/discharge of MOSFET memory devices is 'read'. The 'read' is not speciifcally mentioned in the thesis. But like discharge, 'read' will be addressed as we move from a basic cell to more complex Floating Gate device organization.
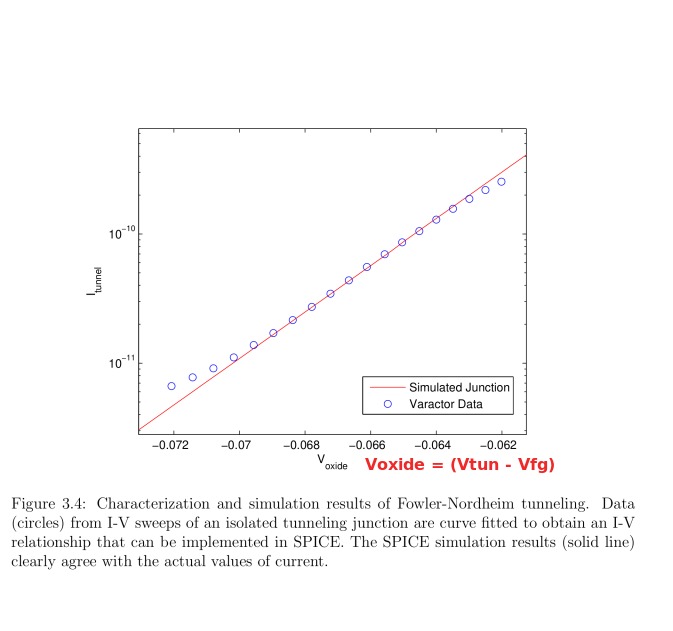
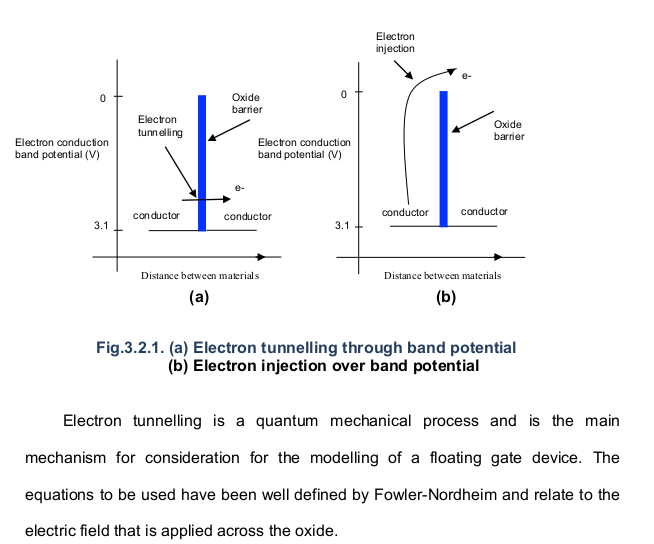
Part 1 page 28 The Fowler-Nordheim appoximation employs two constants that evolve from 'testing' specific MOSFET device 'featrue' physical characteristics.
Merged from Part 1 page 29 Eqn 3.2.1 and page 30 Eqn 3.3.1. Equation 3.3.1 and its derivation form the heart of the thesis and the cell level anlysis/simulation of this project.
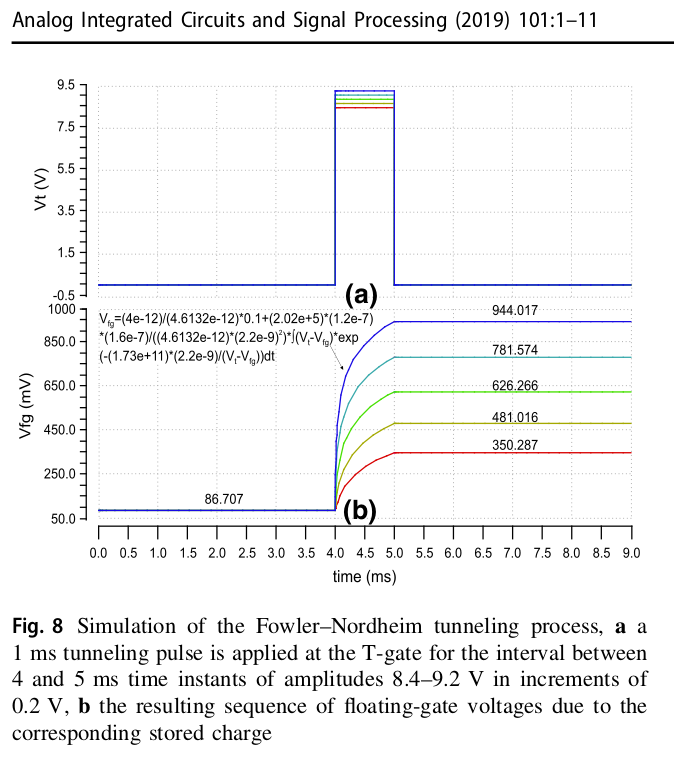
Part 1 page 42..43 Fig 5.1.1(a) and (b) were replicated using 'qucs' to serve as a shke-down curise for the FGMOSFET model and the test schematic. Variations were found. But the model employed was slightly different. The imprtant verification involved the linear and satuttion regions expected charactertics of the FGMOSFET.
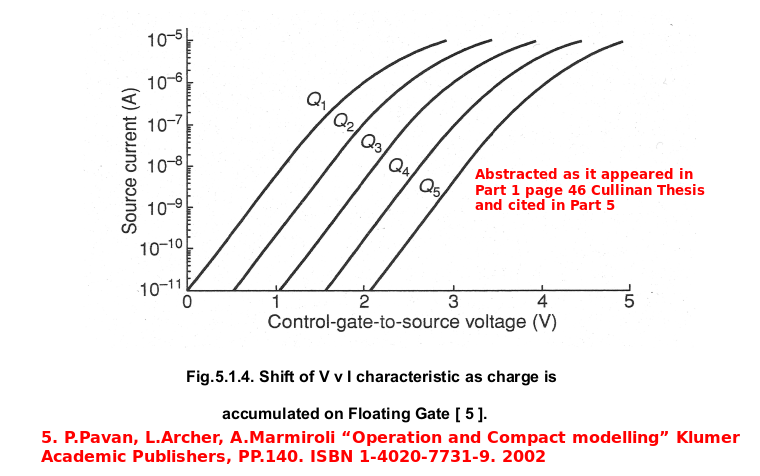
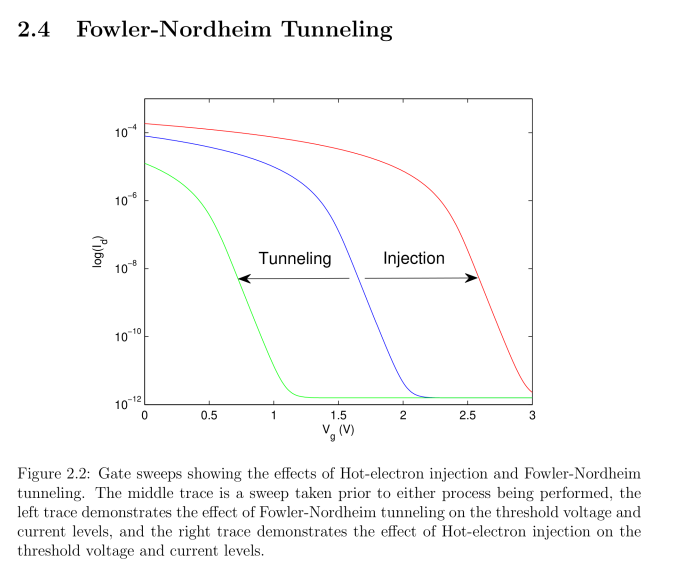
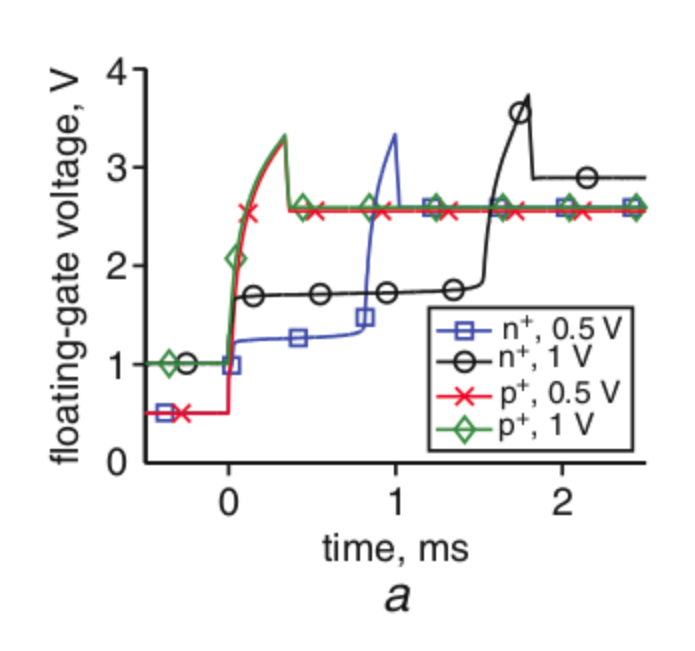
No Image Used Ibid. In Part 1 Chapter 5 page 46 of Cullinan thesis employs a reference used in Cullinan's thesis to the Shift in V-I characteristics as charge accumulates on the Floating Gate appears as it was abracted in the Pavan Team Presentation given further below on this webpage.
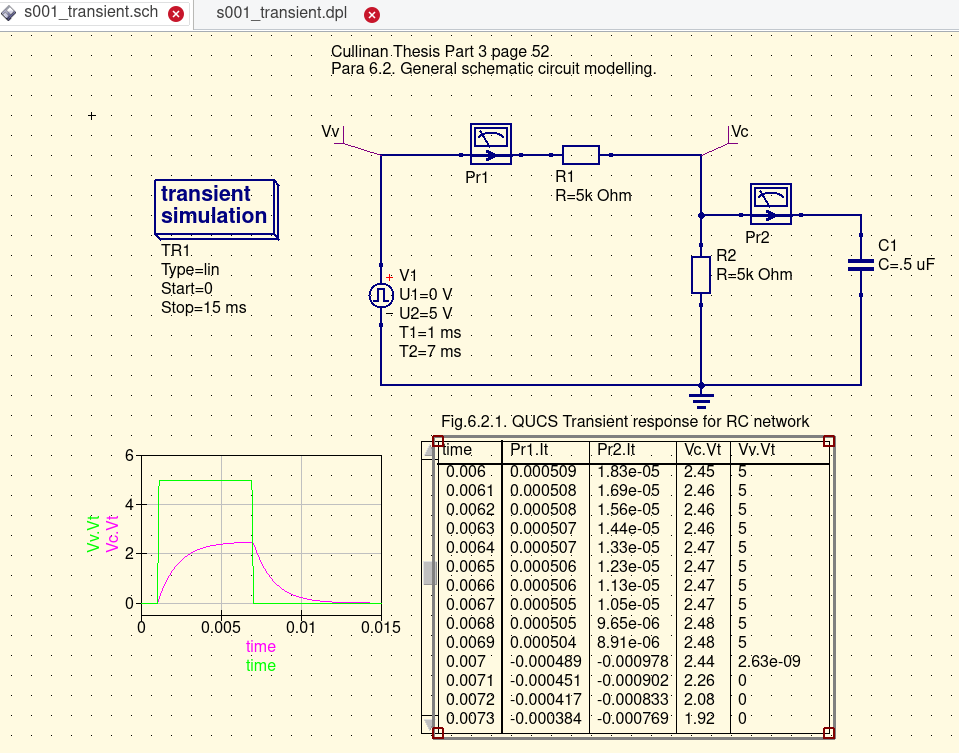
Ibid. Beginning in Part 3 page 52 Cullinan begins to fill the QUCS toolbox with increasingly complex examples of usage of QUCS function and library of devices. This is the part of Cullinan thesis where one needs to return when questions arise.
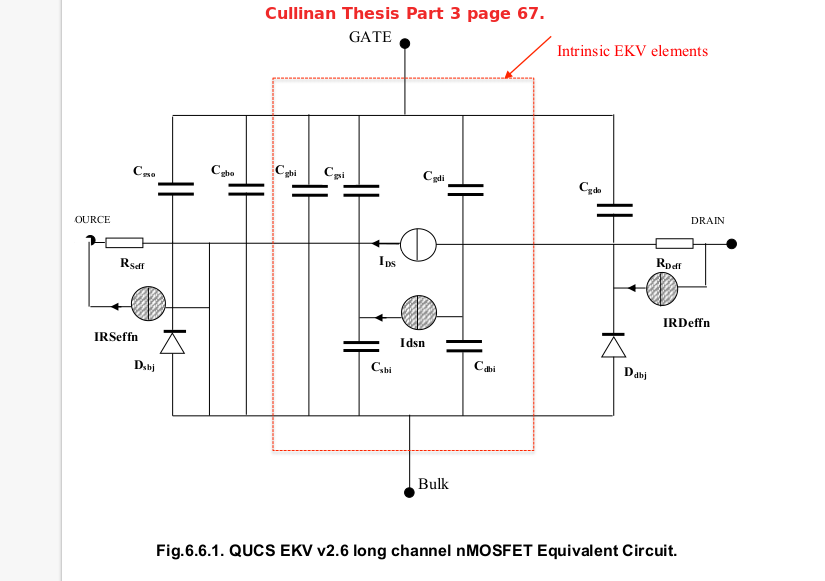
Ibid. In Part 3 page 67 Cullinan begins to made direct reference to modeling the EKV v26 Long Channel nMOSFET device as an equivalent circuirt and a QUCS entity. This divergence between Part 2 and Part 5 provides background needed to understand the schematic/symbol, Equation Defined Devics, subcircuits, transient mode operation, and test congifurations used for simulation.
No Image Used Cullinan Thesis Part 5 plus supporting Abbottanp work product
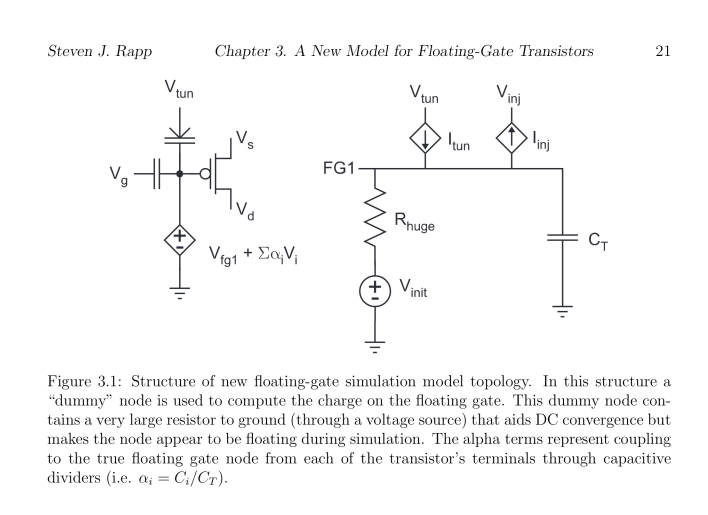
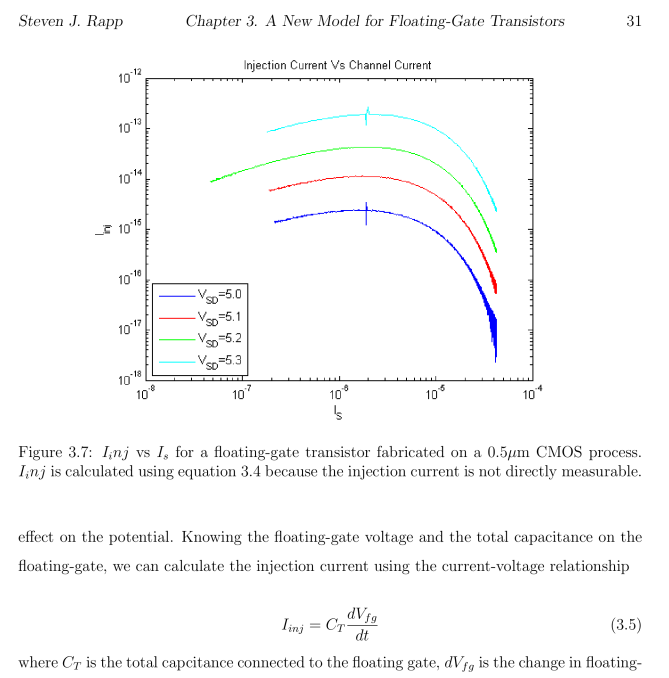
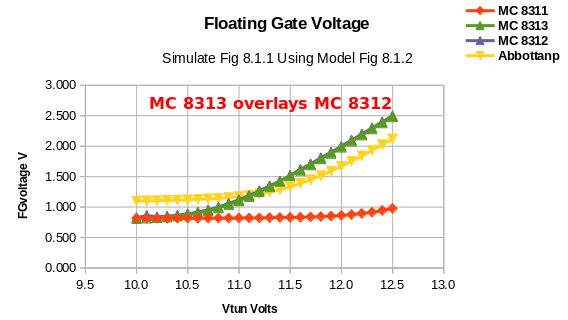
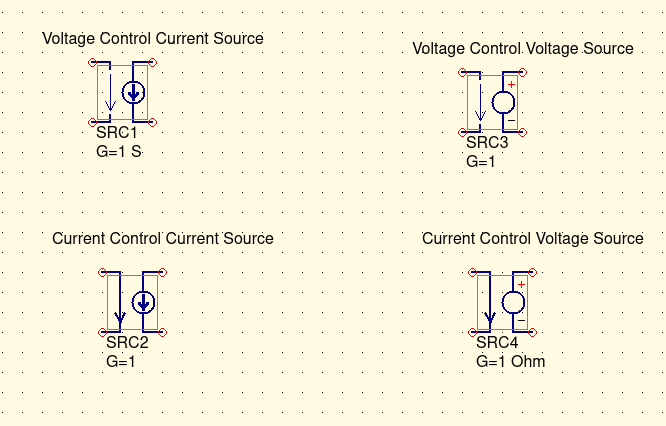
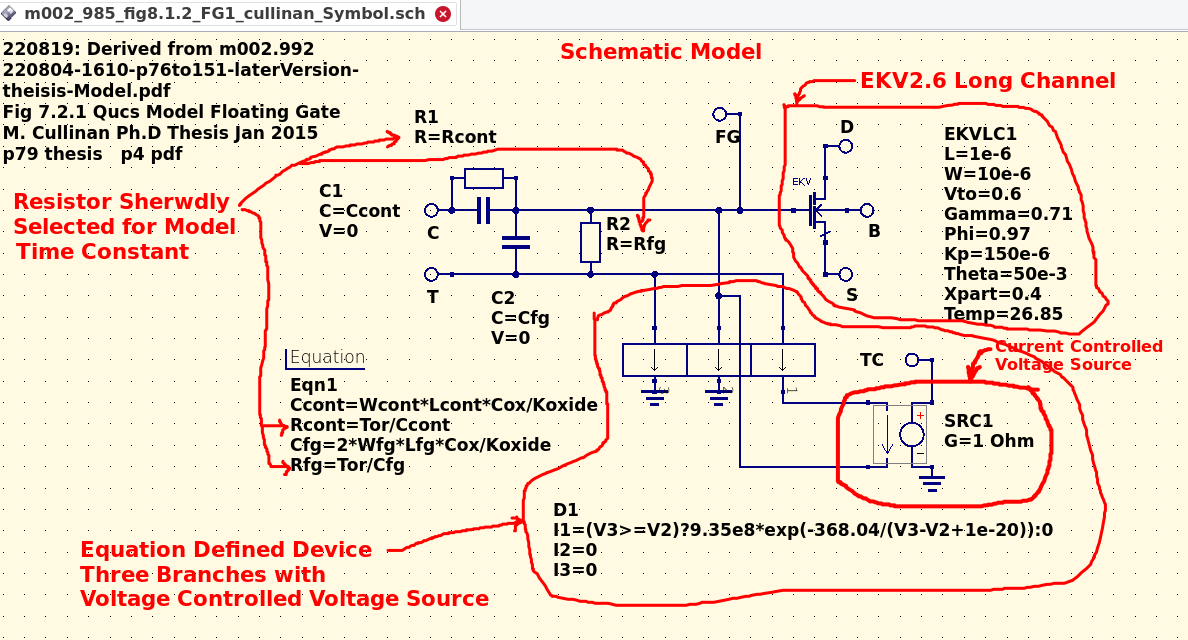
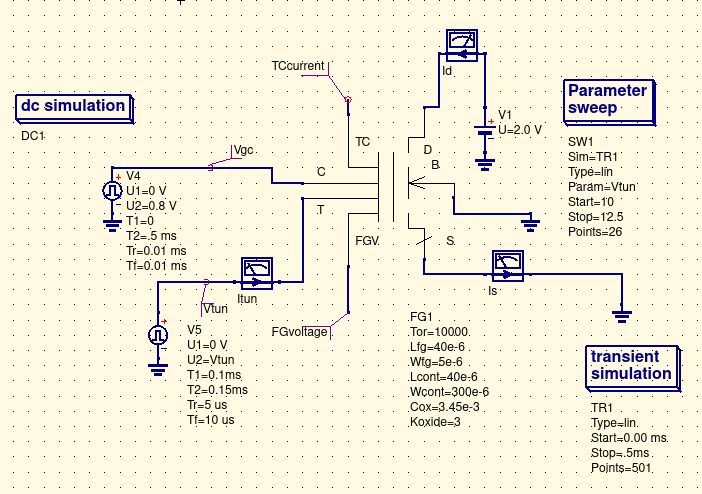
Ibid. Part 5 Page 89 displays Fig 8.1.2 Schematic subcircuit for Floating Gate transisitor, FG1. This schematic presents the QUCS model that Cullinan's Thesis derived from his earleir discussion. It incorporates the EKV26 long channel nMOSFET, the Current Controlled Voltage Source (SRC), Equation Defined Device, as well shrewd usage of time constant resistors. The model graphically shows the 'play of the Fowler-Nordheim equations/constants' with the physical features of the device's width and length.
Schematic With Results

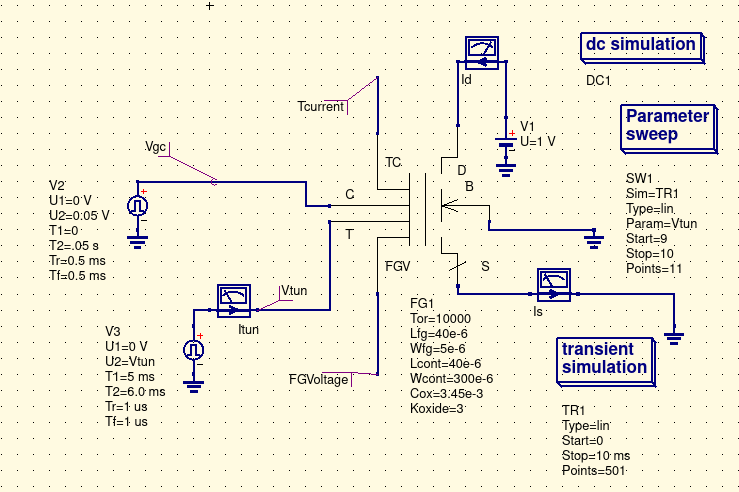
Abbottanp 221029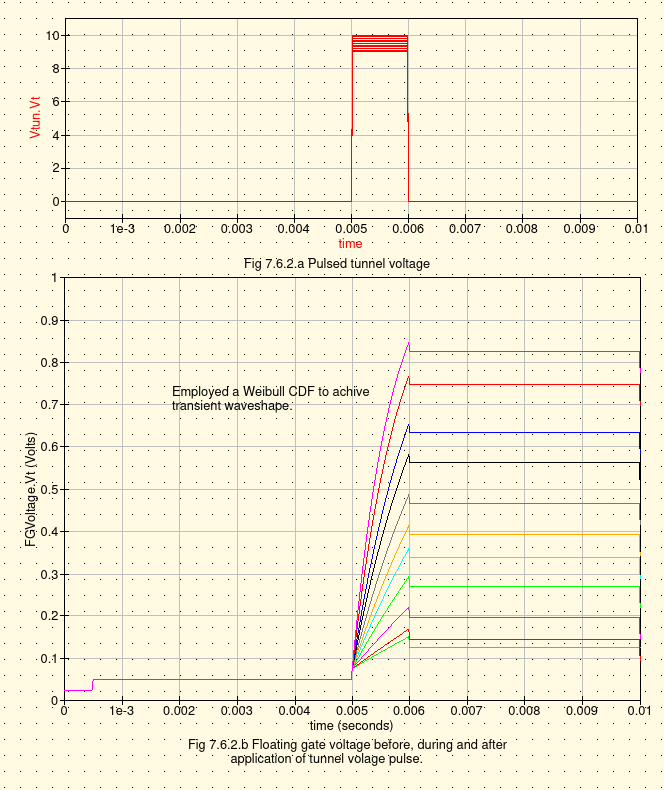
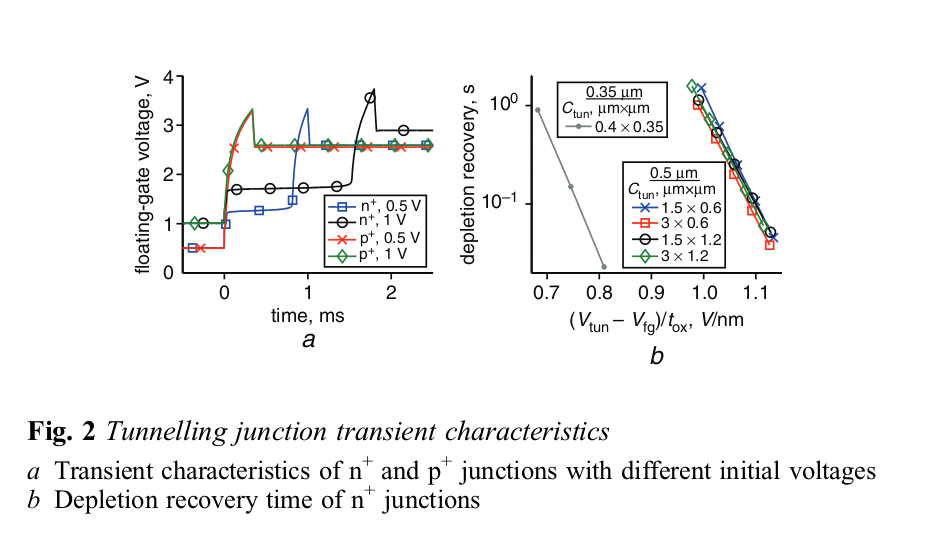
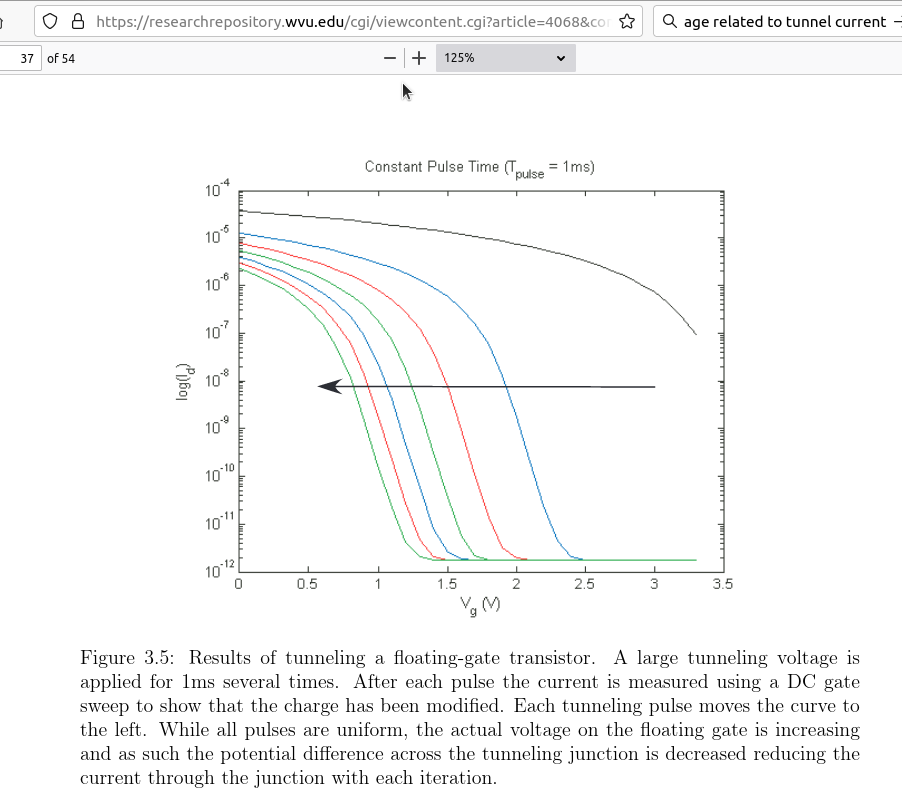
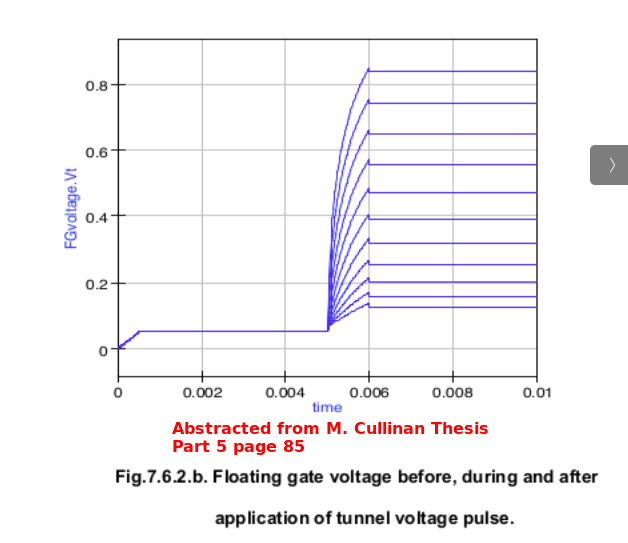
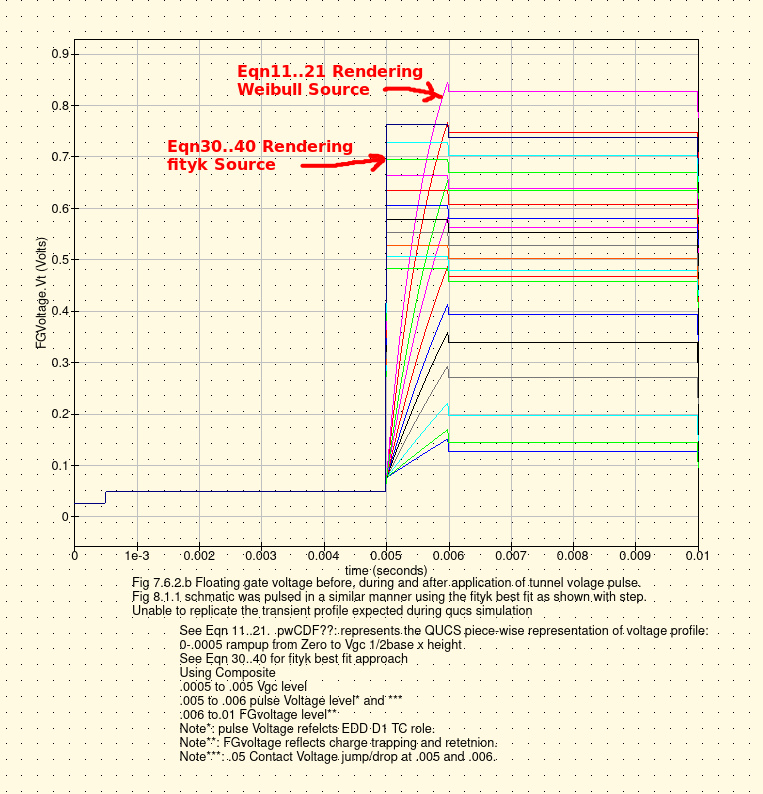
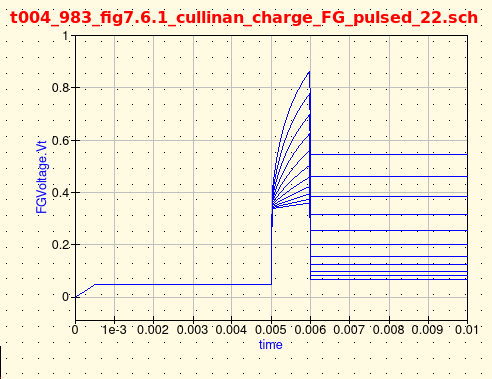
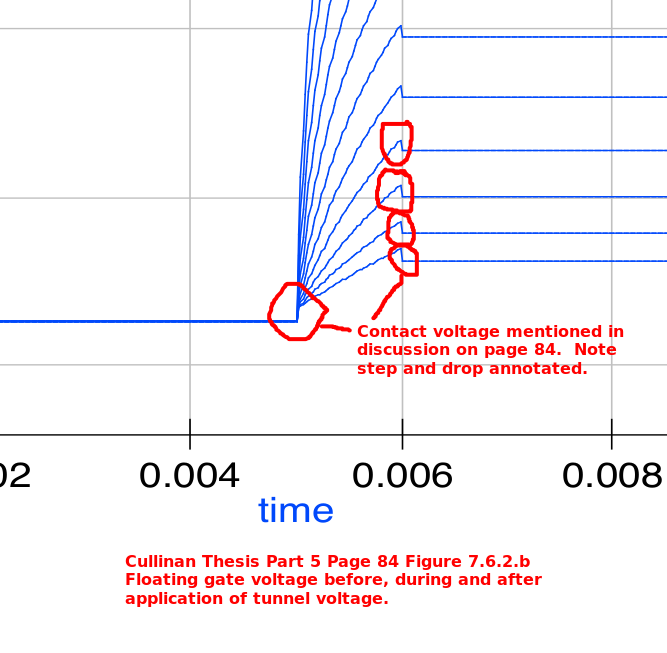
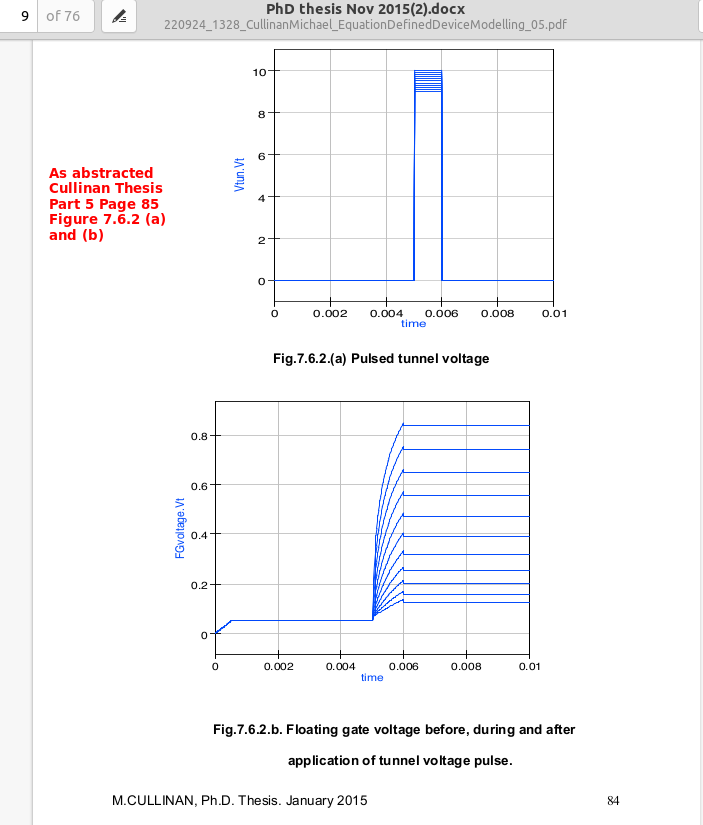
 Ibid. Part 5 page 83-85 Fig 7.6.1, Fig 7.6.2 (a) & (b). The final verification of the schematic, model, and simulation test-beds involved charging the floating gate resulting from pulsed voltages applied at the tunneling port. The simulation results did not mirroed those found in the thesis. Discussion is provided in Issue#1 addressing this anomaly.





See Issue#1 to Consider The expected Floating Gate Voltage profile eluded the qucs simulation of Fig 7.6.2(b).


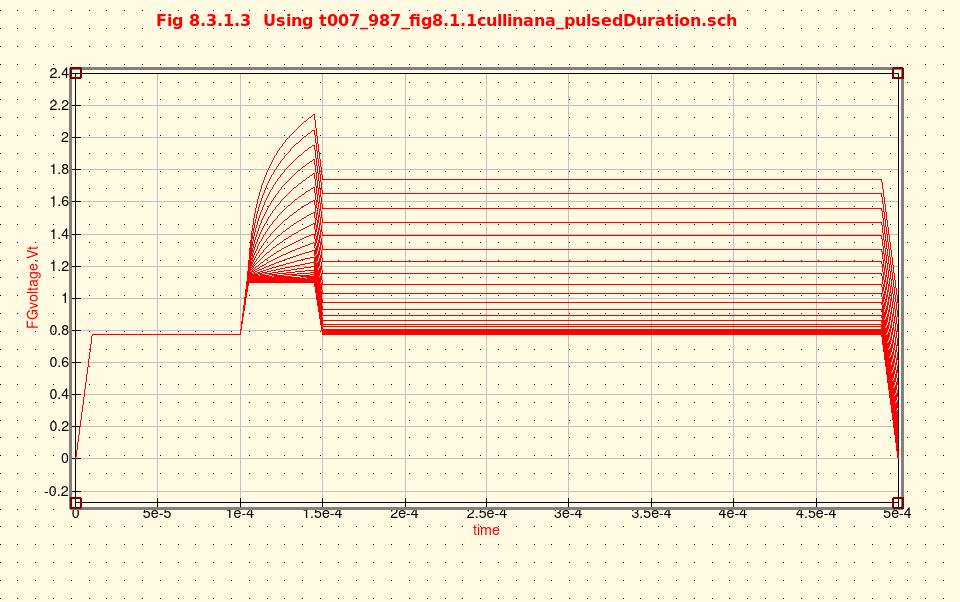
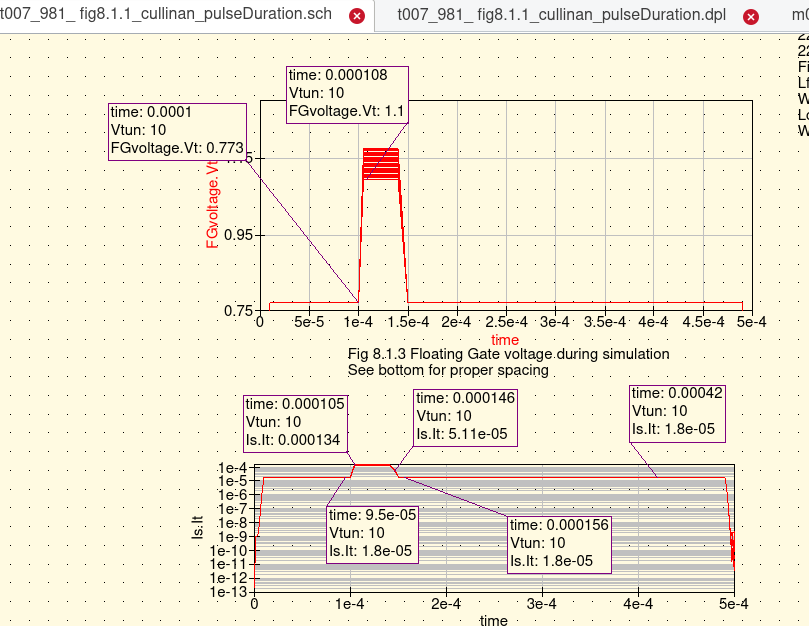
Cullinan Thesis-----Abbottanp
Setup as Fig 8.3.1.3 and Fig 8.1.1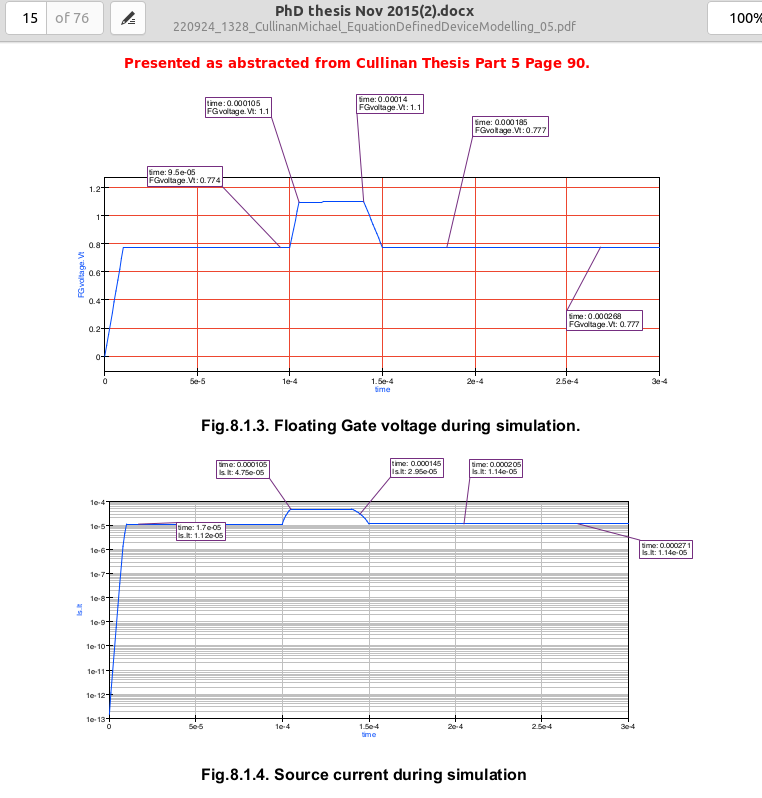


Abbottanp Recalibrate using
V1 = .075 V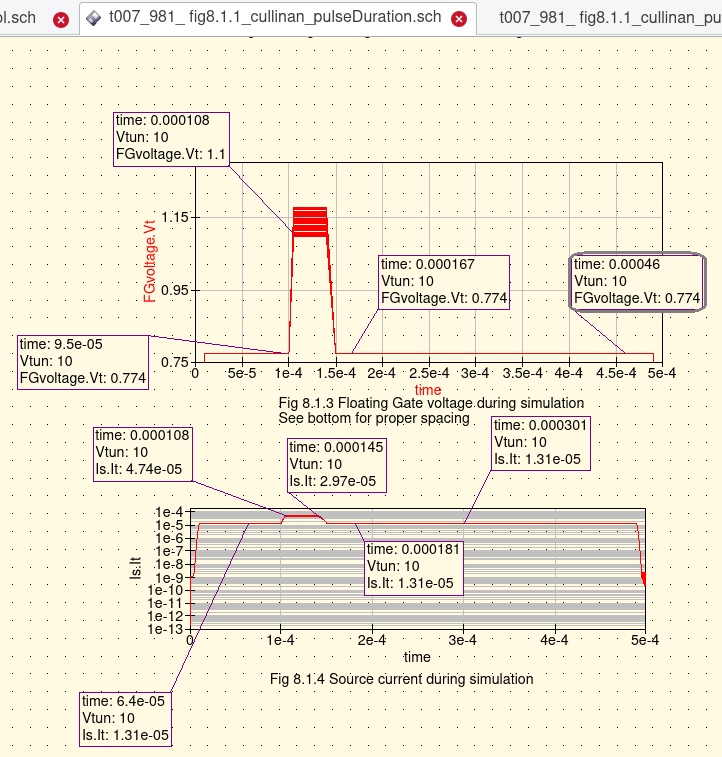
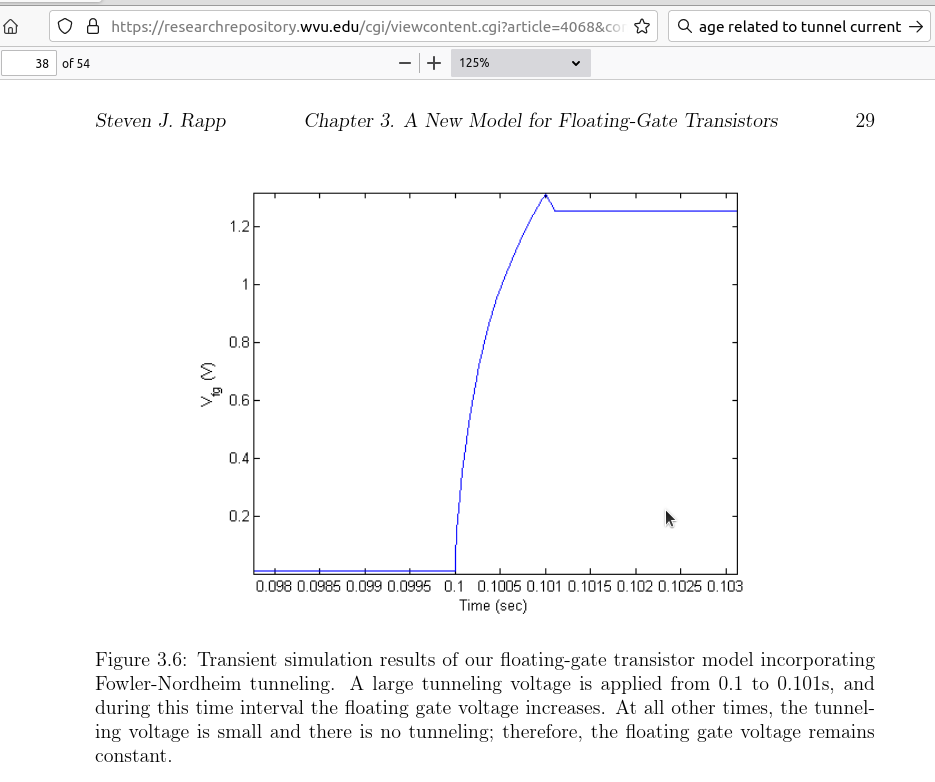
Ibid. Part 5 page 87- 99 Fig 8.1.1, Fig 8.1.2 plus plots labled Fig 8.3.1.1 - 8.3.1.8. The battery of simulations was replicated with 'close' appoximation with the results shown in the thesis. Predicated upon the acceptance of the thesis the presenteed simulation results was accpeted as 'true' for the technoogy and pulse profile specified.

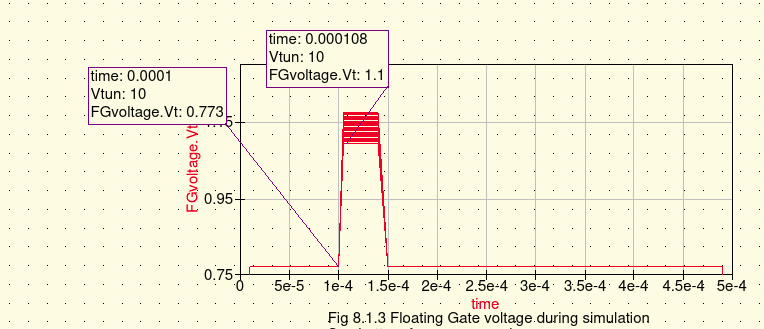
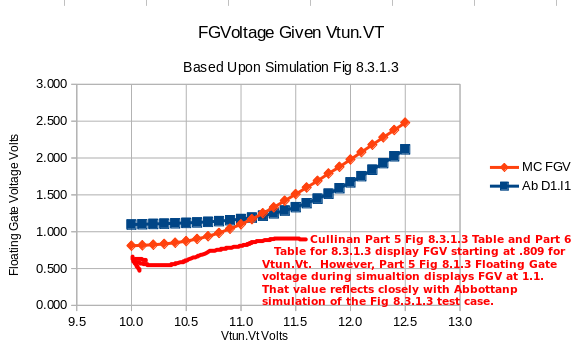
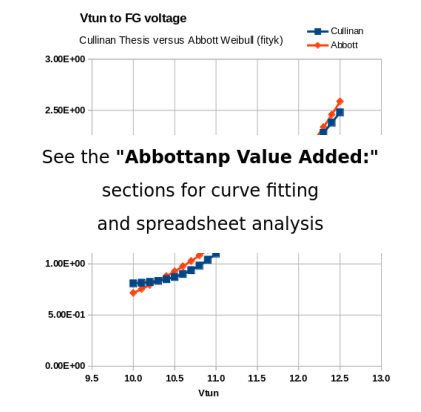
See Issue#1 to Consider The expected Floating Gate Voltage profile eluded the qucs simulation of Fig 8.1.1.1. Abbottanp simulation results for Vfg were not as expected for resulting Figure 8.3.1.1..8.3.1.3. But Figures 8.1.3 and Figure 8.1.4 matched before any best-fit fityk activity was attempted.

To accommodate the 'delta' difference between the Cullinan thesis' data and Abbottanp project's rendering of the simulations, the 'fityk' curve fitting of the Cullinan thesis data was aaumed to be adequate representation of the Floating Gate Voltage (FGvoltage.Vt). With this assumption further work continued to develop a 'workable feel' for a single cell of the Floating Gate Electron Reservoir Power Source as represented as the test-bed and model presented in Fig 8.1.1 and Fig 8.1.2.

Series 2 through Series 4 (Part 5 pages 100-125 remain to be processed/studied. These three series represent special case await investigation as time permits. The three series represent lesser order significance to this project.
Abbottanp Value Added: Curve fitting using fityk submitting Cullinan simulation data for salient test runs. Resulting best fit curves/equations used for FGV, Itun, and Is.It analysis to acquire basic cell ideal charge capacity.
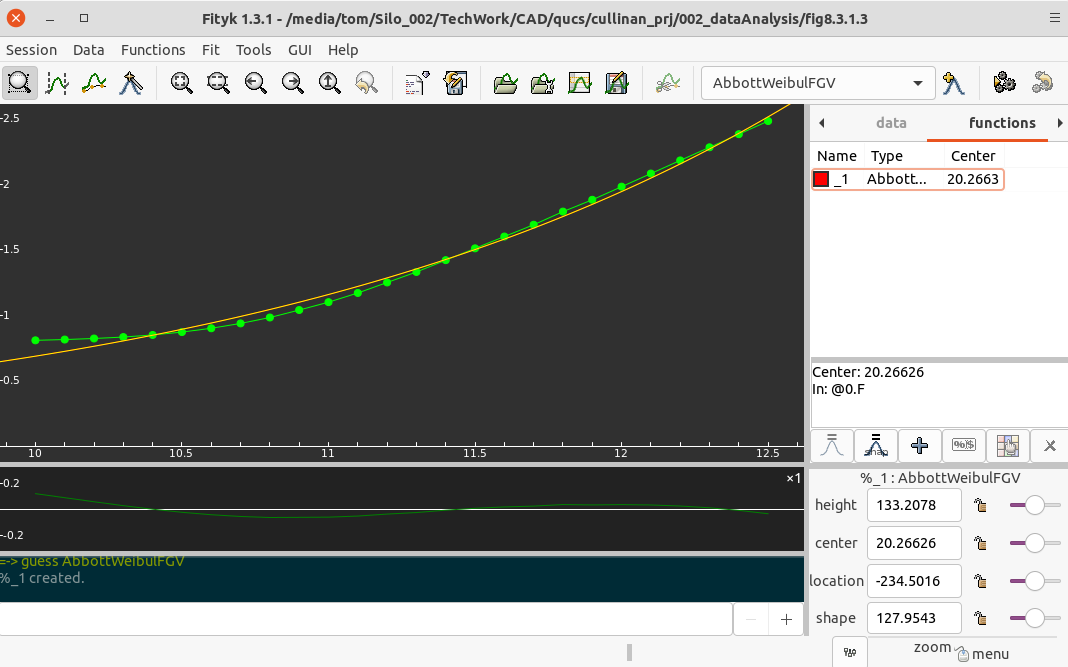
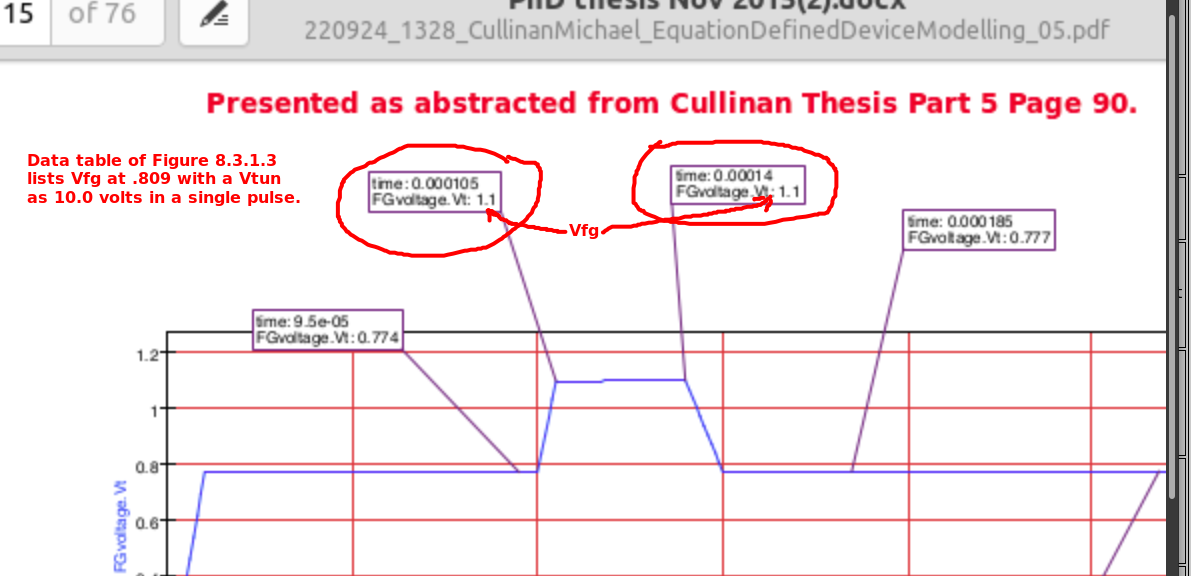
8.3.1.3 Floating Gave Voltage after pulse fall: Curve fitting via fityk yielded equation:
Given Itun A = (x > 9.9999 and x < 12.5001)
define AbbottWeibulFGV(height=133.2078, center=20.26626, location=-234.5016, shape=127.9543) = height * (1-exp(-( (x-location) / (center-location) )^shape) )
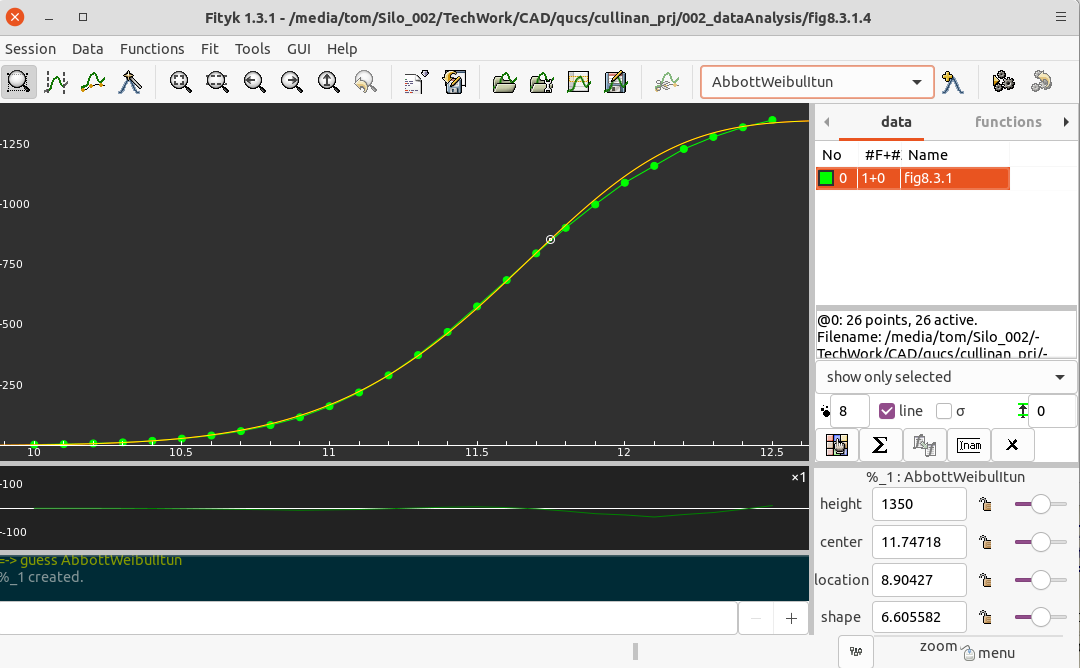
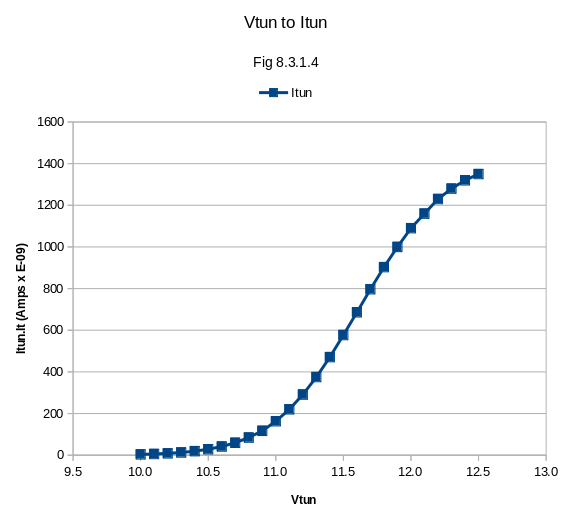
8.3.1.4 Itun during pluse: Curve fitting via fityk yielded equation:
Given Itun A = (x > 9.9999 and x < 12.5001)
define AbbottWeibulItun(height= 1350, center= 11.74718, location= 8.90427, shape=6.605582) = height * (1-exp(-( (x-location) / (center-location) )^shape) )
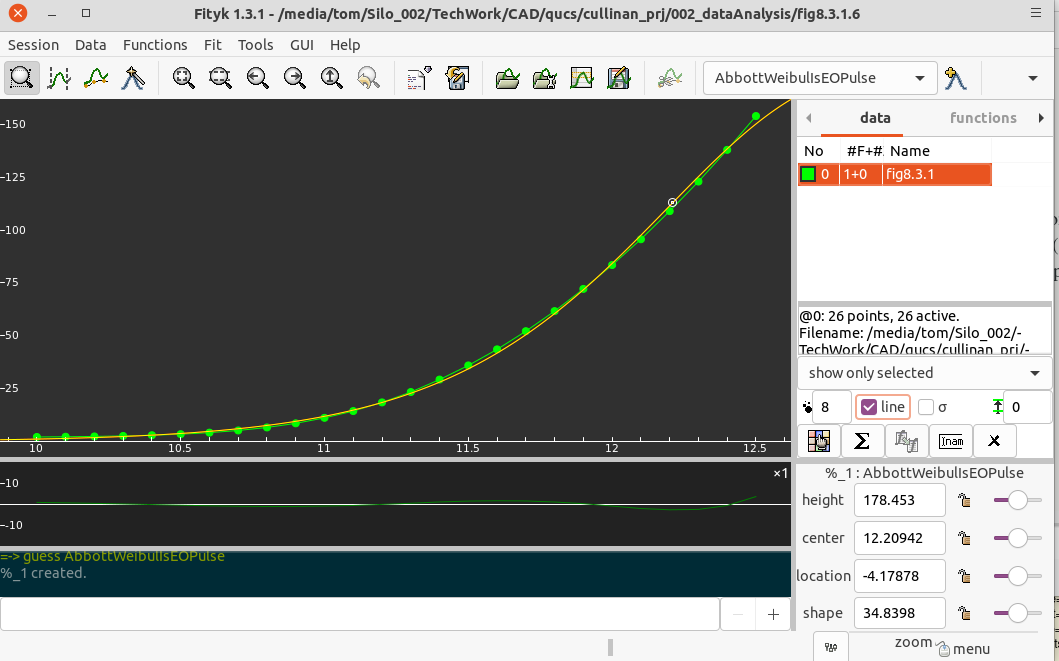
8.3.1.6 Is at end of pulse before fall: Curve fitting via fityk yielded equation:
Given FGvoltage A = (x > .8 and x < 2.5)
define AbbottWeibulIsEOPulse(height= 178.453, center= 12.20942, location= -4.17878, shape=34.8398) = height * (1-exp(-( (x-location) / (center-location) )^shape) )
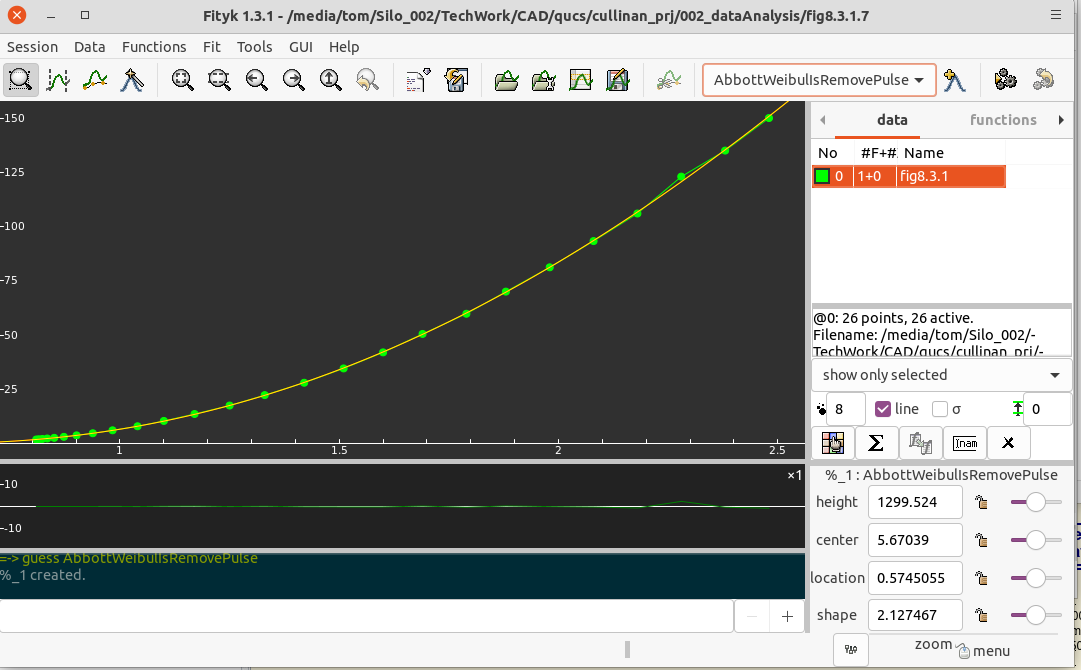
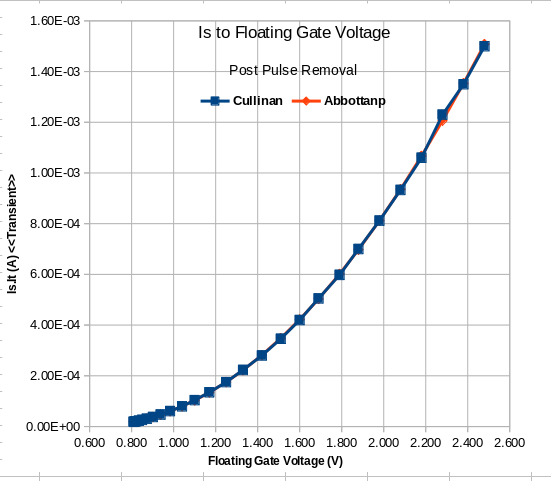
8.3.1.7 Is after pulse removed: Curve fitting via fityk yielded equation:
Given FGvoltage A = (x > .8 and x < 2.5)
define AbbottWeibulIsRemovePulse(height=1299.524, center=5.67039, location=0.5745055, shape=2.127467) = height * (1-exp(-( (x-location) / (center-location) )^shape) )
Abbottanp Value Added: Two separate collections of spreadsheets were produced from the data collected running Fig 8.1.1 and Fig8.1.2 (Abbottanp: m002_985_fig8.1.2_FG1_cullinan_Symbol.sch and t007_981_ fig8.1.1_cullinan_pulseDuration.sch) The data collected (data: t007_981_ fig8.1.1_cullinan_pulseDuration.dat and display: t007_981_ fig8.1.1_cullinan_pulseDuration.dpl) were directly submitted to analysis using spreadsheet 221106_1356_m002_t007_981_wargaming.ods.
File: 221107_*wargaming.ods
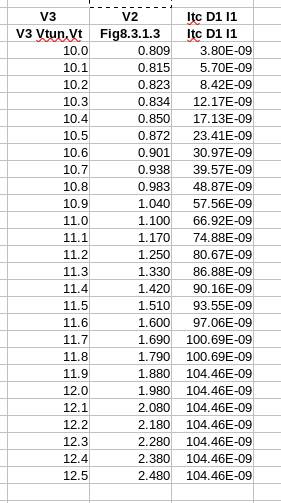
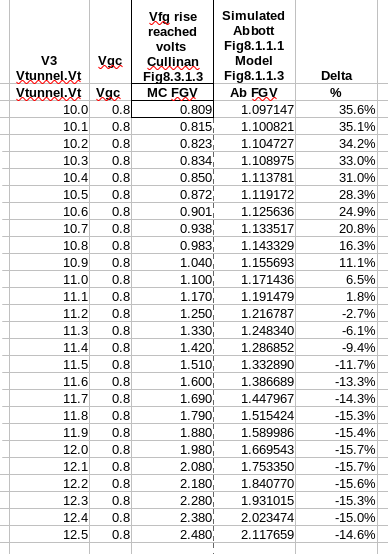
Sheet: m002_985_analysis 		Standalone Analysis m002_985_fig8.1.2_FG1_cullinan_Symbol.sch: A spreadsheet analysis was performed using the EDD (Equation Defined Device) model supporting Fig8.1.1 simualtion testing. The spreadsheet analysis of that data plotted and graphed yielded pawned from the independent variable Vtun.Vt range (10 to 12.5 volts incremented a .1 of a volt) submitted to the Fowler-Nordheim equation as shown in the m002_985_fig8.1.2_FG1_cullinan_Symbol.sch shematic briefly discussed earlier in the Cullinan Thesis.
File: 221107_*wargaming.ods
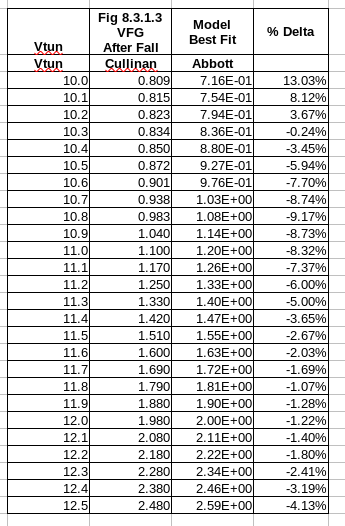
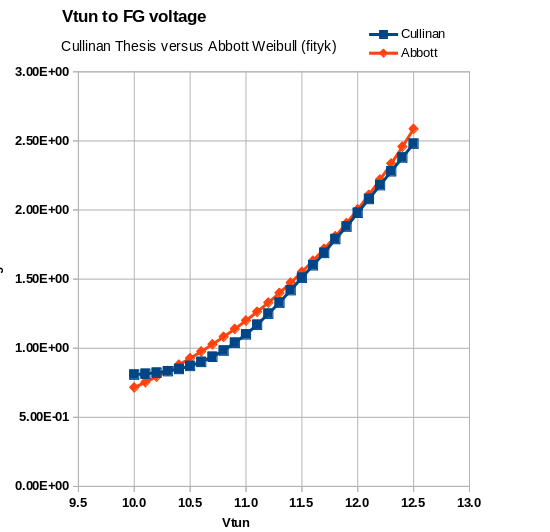
Sheet: Chap8_AbbottWeibull_FGV 		8.3.1.3 Floating Gate Voltage after pulse fall: Spreadsheet analysis provided confidence that the Cullinan data and AbbottWeibulFGV model/equantion where very close appoximations. The 'slope' parameter 127.9543 caused 'floating point' issues with the spreadsheet analysis application. The value 127.0000 usage result in no 'floating point' issue. But it did result in a marginally higher FGV in numerous instances.



See Issue#1 to Consider The expected Floating Gate Voltage profile eluded the qucs simulation of Figure 8.1.1.1 schematic resulting in Figure 8.3.1.3 table of data.
File: 221107_*wargaming.ods
Sheet: Chap8_AbbottWeibull_Itun 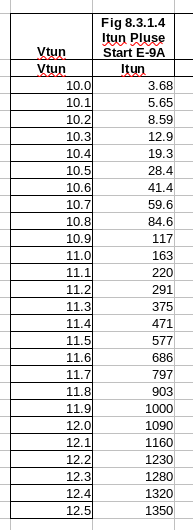		8.3.1.4 Tunnel Voltage to Itun at start of pulse: A spreadhsheet analysis was not pefromed since the fityk curve fitting of the Cullinan thesis showed a very 'tight' fit. This curve was not anticipated to be requred for the next level of analysis.
File: 221107_*wargaming.ods
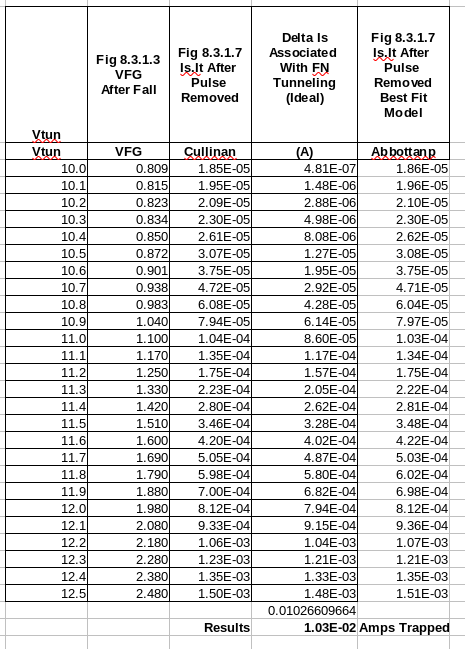
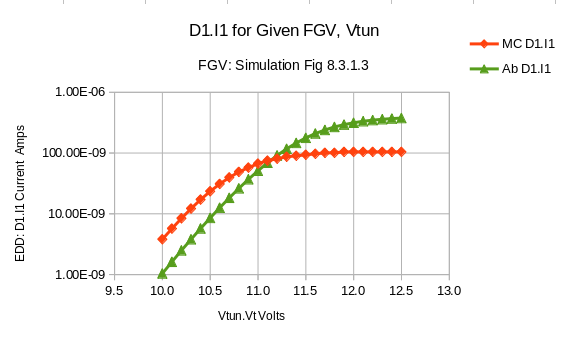
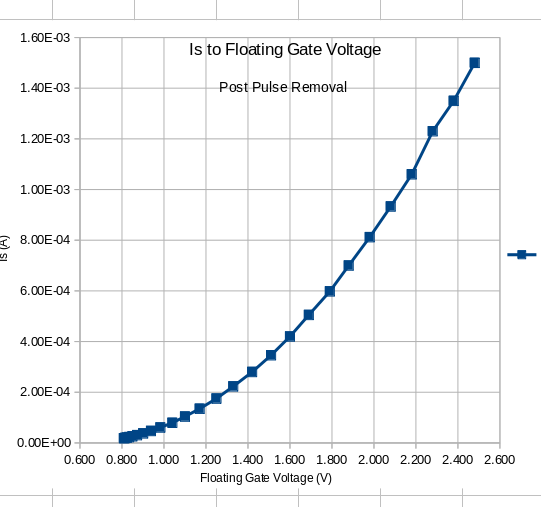
Sheet: Chap8_AbbottWeibull_Is 		8.3.1.7 Is after pulse removed: This is the money-shot''. As such a deeper spreadsheet analysis was performed.

First subset analysis, the delta between Is.It DC/Steady-State and the Transient mode was determined for for each Floating Gate voltage (between .8 and 2.5). The 'delta values were collected in a 'bucket' and a summed. The resulting value was 1.03E-2 Amps trapped in the Flaoting Gate. The conversion task to Charge was planned to be performed in a separate analysis which follows shortly. The results sugest the current that can be trapped within a Floating Gate Electron Reservoir Power Source basic cell.

Due the cirticality of this set of spreadsheet analysis, the second subset analysis was requred to demonstrate that the fityk best fit curve closely reflects the Cullinan test data. The correcponding plot clearly show a very, very tight fit.
File: 221107_*_stateMachine.ods
Sheet: Calculate
Standalone Analysis Using Chap8_AbbottWeibull_Is Results: Assuming that the Cullinan-Abbottanp analysis stands peer-review, the results: charge can be trapped within a Floating Gate Electron Reservoir Power Source basic cell is converted to Charge expressed as electron-volts. The number of basic cells required to build an 80KWHr loating Gate Electron Reservoir Power Source entity was calculated and displayed in the spreadsheet analysis. No assumption was made at this point about technology feasibility, power supply efficiency, reliability, etc.
TBD








Pavan and Team Presentation:

Image Comment
Model proposed by Pavan and Team "Floating Gate Devices: Operation and Compact Modeling". The Pavan team's presentation proposes a model which addresses both DC and Transient operation. Cullinan's thesis draws heavily from the formal publication of the Pavan's team work.
Ibid. The Pavan Team introduces the complex nature of 'corraling' the Charges involved in a Floating Gate MOSFET.
Ibid. The Pavan Team proposes a model to use to determine the associated Floating Gate Voltage, Vfg.
Ibid. The Pavan Team presentation introduced the voltage controlled current source as the significant entity employed to simulate the Transient operation of a Floating Gate MOSFET.
Ibid.The Pavan Team suggests a methodolgy for calculating Vfg, floating gate voltage using the error prone concept of capacitance coupling coefficeints, αi = Ci/CT.
Abstracted Pavan Team work as it appeared in Cullinan Thesis Part 1 page 46, Fig 5.1.4.
TBD







Salient Abstracts:

Image Comment
Rumberg and Graham's paper, "Efficiency and reliability of Fowler-Nordheim tunnelling in CMOS floating-gate transistors," appearing in ELECTRONICS LETTERS 7th November 2013 Vol. 49 No. 23 pp. 1484 employed a schematic and equvalent circuit which yielded data results (Fig 1a..1d) similair to results obtained via Cullinan Thesis simulation. A brief discussion of programming, erasing, and reading the floating gate was also found to be helpful.

Rumberg and Graham's article goes a long way summarizing Cullinan's Thesis analysis and simulation process. The most signifcant difference between Rumberg/Graham presentation and Cullinan's Thesis is that Rumberg uses p-MOS while Cullinan uses n-MOS technology. No preference is endorsed or advocated at this junction in time.
Ibid. The discussion presented in the article links the FN manufacturing technology alpha and beta parameters to the Itun current in a manner similar to Cullinan.
Ibid. The floating gate voltage due to transient mode reflects the same shape and capacitor charge impact as shown in Cullinan's Thesis.

The remainder of the article 'suggests' strategies (pp 4185 and 4186) which may be useful for enhancing the efficiency and reliability of the Floating Gate Electron Reservoir Power Source. Further discussion at this time is beyond the scope of the project.
Steven Rapp, "A New Modelfor Floating-Gate Transistors" page 7 Section 2.4 Figure 2.2 with discussion of Fowler-Nordheim tunneling/injection impact of the threshold voltage.
Ibid. page 21 Chapter 3 Rapp introduces a FGMOSFET model from which he proceeds forward with his simulations. Like Cullinan's Thesis a voltage controlled current source plays a key role in applying the proper amount of charge on floating gate node.
Ibid. page 26 Chapter 3.
Ibid. page 28 Chapter 3. Figure 3.5 reflects the effect of tunneling on the Floating Gate devcie.
Ibid. page 29. Fig 3.6 exhibits a similar profile to that shown in Cullinan thesis. Rapp's follow-up discussion explains the charactertistic found in the profile, the self-limiting aspect of Vfg, charge storage, and effect of capacitive coupling..
Ibid. page 31. Figure 3.7 appears with an explanation of the governing Iinj current Equation 3.5.
Ibid. Chapter 3. Rapp presents two figures Figure 3.8 and Figure 3.9, predicated upon 0.5um CMOS processing technology. Together they document the emprical relationship Rapp pursued in this work.
Haifa Abulaiha, "Programming of Floating-Gate Transistos for Nonvolatile Analog Memory Array", Chapter 2 page 11 Fig 2.5 depicts the where "Injection programming adds electrons to the floatin-gate, while tunneling removes electrons from the floating-gate."
Paul Hasel, "Floating-Gate Devices, Circuits, and Systems", Proceedings of the 9th International Engineering & Applications Symposium, IEEE 2005 introduces earlier prior work of his with Equation 6. This equation shows the self-limiting effect of Vfg on the Itun current.
Ibid. Figure 3(c) with supporting images a, b, d, e displays the V-I characteristics involving injection and tunneling.
C. Zhang and R. Hasan, "A new floating-gate MOSFET model for analog circuit simualtion and design", Analog Integrated Circuits and Signal Processing, 2019 Figures 8(a) and (b) as well as Table 1 compliment the Cullinan thesis. The Zhang and Hasan work also presents device physical dimension features and relates them to engery band. Their presentation like Cullinan's closes with an OpenSource model that supports simulation. Unlike Cullinan work they employed MATHAB instead of 'gucs' and compact EDD. Zhang and Hasan's model presentation is eleven pages long. Cullinan's thesis is well over 120 pages and goes into significant "how-to" detail. Zhang/Hasan model employs a five port model while Cullinan's model employs seven ports. The difference in ports is due to Cullinan's usage of the qucs Equation Defined Device technology and usage of the EKV transistor in simulating the FGMOSFET behavior. Discussion of the 'best' simulation model was settle early in the Floating Gate Electron Reservoir Power Source project boundary criteria of "free is best". The Zhang Team's greates contribution to the project was in helping to clarify and verify the 'thinking' that was associated in the work of the prior authors.


See Issue#2 to Consider The although an energy gap discussion and figure are presented by the Zhang article did not profile the contact voltage, capacive coupling step/drop shown in associated transient mode Vfg profile figures described by other authors.
Ibid. The Zhang Team employs a FGMOSFET equivalnet circuit just a bit different that that used by Cullinan in his thesis. But like Cullinan the focal point of the circuit is the isolation of of the the floating gate and Vfg.
Ibid. With the FGMOSFET equivalent circuit estahished the Zhang Team borrows heavily from Cullinan's laying down the foundation for determining Vfg.
Ibid. The Zhang Team article presents a well reasoned approach combining emprical test data with citing a contribution from Cullinan Thesis among others in an effort to reduce the complxity of modeling Vfg and Qfg.
The Money Shot
Ibid. The Zhang Team draws the MONEY SHOT from their FGMOSFET equivalent circuit through Cullinan's earleir work to a complexity reduced specification of Vfg and Qfg.


See Issue#3 to Consider There may be minor typo involving Eqn 7 and its presentation in Figure 8(b).
TBD
TBD
TBD













Issues to Consider:

Image Comment
Issue #1 Unable to Confirm Floating Gate Voltage

Cullinan



Rumberg



Rapp



Zhang

Issue 3: Minor Vfg profile delta. 		Although multiple references were locate which provided documentation showing a classic transient Floating Gate Voltage (Vfg) profile, during the Abbottanp QUCS simulation the restulting test data did not yield an exact matching profile reflective of the four references. The following three observations can be made regarding the simulation profiles.

First Observation: The shape of the Abbottanp QUCS profile does not closely match any of the documented Vfg profile shapes. But the Abbottanp QUCS profile does exhibit a classic rise at the expected time, a classic drop at the expected time followed by the classic retention projection of the Vfg.

Abbottanp 221220 'creative' simulation using t004_983_fig7.6.1_cullinan_charge_FG_pulsed.sch closely mimic Cullinan Thesis Vfg profile. But Abbottanp 'creative' simulation results are not based on deviced simulation.


Profile Shape
Cullinan Creative &
Best Fit 		Abbottanp
Sim Results 		Abbottanp
Sim Results



Second Observation: The values of the Abbottanp QUCS derived Vfg from simualtion are roughly 35% to -15% delta than those appearing in the Cullinan Thesis.


Abbottanp 221220 simulation using t007_981_ fig8.1.1_cullinan_pulseDuration.sch successfullymatched the Cullinan Thesis Fig 8.1.3 Vfg. But neither matched the Cullinan table results shown (Part 5 Fig 8.3.1.3 table or Part 6 table for "Vfg after pulse fall").

Cullinan-Abbottanp fg Match and Mis-Match
Cullinan
Fig 8.1.3 		Data Delta
MC & Ab 		Abbottanp
t007_981_*



Third Observation: The Cullinan Vfg data difference data tables of Part 5 amd Part 6 with Part 5 "Fig 8.1.3 Floating Gate voltage during simulation" are mildly troubling. Both the rendrings of simulations (Cullinan Thesis and Abbottanp) have mutually supporting plots for Figure 8.1.3 and Figure 8.1.4 . As shown above in the two 'clipped' plots of Figure 8.1.3 the Vfg dervied over the simulation match exactly. However, the data points marked in the Cullinan Thesis Figure 8.1.3 do not appear to match the corresponding plots of Vfg. This same observation holds true in the summary table provided in Part 6. Part 6 page one also seems to have inadvertly drop the last three rows of data for Vtun 11.2, 11.3 and 11.4.

Path Forward: Until such time as new information is available the Vtun data presented in the Part 5 Fig 8.3.1.3 table or Part 6 table for "Cullinan Fig 8.3.1.3 Vfg after pulse fall" will be assumed to be correct. This assumption will lead to a conservative behavior model, results, and estimates/predictions. That model can be tweaked as information becomes available.

The impact of this assumption can be viewed by clicking here or by viewing the Vfg and EDD current images shown below:

Projected Impact of Conservative Vfg
Vfg
Fig8.3.1.3 		EDD
D1.I1 		Vfg
Fig8.3.11..3


Issue #2: Minor Delta between Authors, Floating Gate Voltage Profile

Cullinan Contact Voltage
Rapp Discussion
The model presented by the Zhang Team deviated from other authors by not reflecting the step and drop in the Vfg profile. See Cullinan Thesis Part 5 page 85 (abstract shown in the column to the immedaite left) for a brief discussion of this quantity as contact voltage during transient mode operation. Rapp presents a brief discussion of this step/drop as being assoicated with capacive coupling from the tunneling voltage through the tunneling junction (Rapp pages 29..30) resulting from transient mode operation. Rapp further eludes to Table 3.1 in a discussion of a quantity termed αx = Cx/CT. This usage of α ties directly to the Eqn 3 of Zhang's Team presentation.

But as with all the supporting authors there is agreement that once the Vtun is withdrawn the Vfg goes flat and remains in that condition.
Issue #3: Difficulty Employing Equation

Equation 7: Defining Vfg.



Equation in Figure 8(a): Parameters loaded post integration.

Vfg = Kcg + Kfg ∫t1..t2 Kae dt
Observe: ∫ a dt = a t + C
where C is an integration coeffiecent that cancels when solving for integration between t1 .. t2.


Assumes Vfg at t1 is defined as Vfg1


Then
Vfg = Kcg + Kfg * [(Kae*t2) - (Kae*t1)]

Collecting terms:
Vfg = Kcg + Kfg Kae* [t2 - (t1)]

Vfg = CcgVcg/CT + ρWTLT/CTT2ox * (Vtun-Vfg1)2 * exp(-(θ Tox)/(Vtun-Vfg1)) * [t2 - (t1)]

where:
Kcg = CcgVcg/CT
Kfg = ρWTLT/CTT2ox
Kae = KaKe
Ka = (Vtun-Vfg1)2
Ke = exp(-(θ Tox)/(Vtun-Vfg1))

View paramters:

Point of Note
Both Cullinan's Thesis and Zhang's Team presentation strongly suggest and support self-limiting aspect of Vfg using the (Vtun-Vfg) relationship (See Cullinan D1.I1 equation and Zhang's Eq7 both referenced previously Cullinan and Zhang repectively). Rapp's Thesis (26-30) provides an excellent extended discussion of this self-limiting aspect of the Vfg parameter in the transient mode operation that incorporates the Fowler-Nordheim tunneling process. Hasel clearly shows the self-limiting aspect with his introduction of Equation 6 during his discussion of the physics behind floating gate tunneling.

TBD












Ash And Trash:

Image Comment
Care must be taken to insure that the correct dependent source is employed. Abbottanp started down the "primrose path" with a voltage controlled source only to painfully discover that a current controlled voltage source was to be employed. Graphic-wise the two dependent source devices are given in the QUCS library as the same figure but with different G: gain factors.
The following sources of information concerning Current Controlled Voltage Sources are provided. This is not an exhaustive list nor an endorsement.
TBD
TBD
TBD
TBD









NOTICE: This site was fabricated for best viewing using Netscape 4.x, or a functionally equivalent browser.

Please send comments or questions using e-mail, voice telephone at 919-846-7705. (Last update: Dec 21, 2022 tar)